Machine Learning is aimed at configuring system to maximize feedback from environment. The general idea is presented below
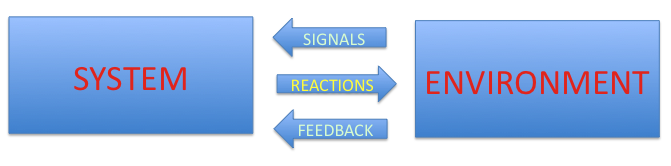
System obtains some signals from the environment. Next system answers (reactions) to the incoming messages are sent back to it. As a next step system reactions are judged by the outer system. When system outputs are correct environment pays profits to it (positive feedback) otherwise system is punished by the signals sender and gets its negative feedback. This is a sign that something works wrongly and needs to be correct.
System is completely defined by set of classifiers (rules). Each rule contains a pair of condition and corresponding system answer when this condition is satisfied.

Conditions are written as strings built with signs from the set of {0, 1, #}. The first two symbols has clear meaning whereas the last one denotes an undefined sign that can be interpreted either as 0 or 1.
Answers are written as strings with signs from the set of {0, 1}. It means that there is no place for free translation. The system answer causes a well-defined action detected by the outer system.
Note. In the OptFinderML, classifiers (rules) must be set by an user. It can be done:
Surroundings (environment) is an outer structure that teaches our system how to react correctly to signals acting as stimuli. Therefore this structure must
a set of inducements (signals) and expected answers (actions).

Signals are sent to the system that generates answers. When obtained reply to given stimuli is correct environment pays a prize to the system otherwise the system pays a fine.

Signals are written as strings built with signs from the set of {0, 1} and are sent to the system each dt - a time step used in further calculations. System detectors register messages and write them to a file or environmental messages can be written to a file directly and then picked up by the system.

All classifiers are matched against detected signals. Each single signal is checked with each condition in the set of all system rules.

If a message matches a condition pattern it is allowed to attend an auction. By the auction the right to possess this signal can be sold according to one of the schemes:
The first auction plan is clear. The winner will activate the appropriate action being its (and system) answer to that message. The second method can be associated with the internal flow of information as a cascade: message - action(s) - message - ... - a single winner (final ACTION). This internal flow of inputs and outputs lasts as long as a single winner will be reached.
Strength of a rule reflects its quality. The higher strength value the better rule. A classifier's strength value is not constant but varies in time according to the auction results and can be represented by equations
| sij = si-1j + Δsm = si-1j + | ∑ | bid(sik) |
| k |
| sij = si-1j + Δsp = si-1j - | ∑ | bid(sik) |
| k |
where si-1j and sij are strength values for the j-th classifier at (i-1)-th and i-th moments in time, respectively. Initial values of si=0j for each j must be set.
Auctions are run with prices offered by selected classifiers. A classifier's bid is not any price that could be thought but depends on a variable s (strength) reflecting rule's quality. The higher s value the richer rule. It means that its ability to buy goods (signals) is high.
where si is the strength of i-th classifier, a0 is a constant and dt is a time step. Bids are calculated in such a simple way since a purely deterministic mechanism is assumed as a governing law. However, classifier's offer can be additionally modified by some random fluctuations. Then the total bid value is computed according to the following equation:
where si is the strength of i-th classifier and random() function can be built from the following types of noise
where ai coefficients are constants and
When a bid value is calculated then both an elementary tax and a bidding tax are collected. They values depend on a variable s (strength). The elementary tax is gathered from all rules in the system
while the bidding tax is charged to those classifiers which sold signals
where sij is a strength of j-th classifier at i-th moment in time ael is a tax coefficient for the elementary tax, abid is a tax coefficient for the bidding tax and dt is a time between successive outer (environmental) messages.
System answer to incoming signals must be judged by the sender. It means that there is a map of signals and corresponding proper answers. If environment obtains answers it must take an action. A correct answer causes payment leading to increase a value of a correct classifier whereas a wrong one causes a financial punishment decreasing rating of a bad one. Either a prize or a fine can be set as constant value or calculated from a receipt similar to that in the System Payments including both deterministic and random parts in the total payment (+) and charge (-) value:
where dij is a deviation from the correct answer for j-th classifier at i-th moment in time, b0 is a constant and random() function is built from the following types of noise
where bi coefficients are constants and
For a proper work of a machine learning system synchronized communication between the system and the outer environment is crucial. The optfinderML provides users with internet services available in two modes:
Time Series Analysis can be performed via three main approaches depending on time series origin:
Genetic algorithms (GA) approach is applied for performing a selection among a set of rules as well as introducing a certain level of rule's diversity in order to tend towards the maximum of environmental feedback. Genetic algorithms can be divided into two main groups of haploid and diploid type. Both genetic models deal with populations of sequences of ternary digits {0, 1, #} (rules conditions). Each sequence represents a condition written as
Information from the genotype (=condition) is used in the matching procedure. To every genotype is assigned a numeric value being the genotype's strength. It can be modified by auctions. The genotype's strength (=classifier's strength) is equivalent to the fitness function in genetic algorithms. The fitness function is the essential measure of chromosome strength to occur in the next generation. The higher fitness of chromosome the greater chance to reproduce. Reproduction in population is thought as a randomized process based on the fitness function. Only these chromosomes that are selected can take part in producing the next generation. The reproduction algorithm is based on the de Jong's crowd model.
In haploid models, a pair of chromosomes is a pair of parents that exchange their genetic information through the crossover process whereas, in diploid models, the process of gametogenesis uses the crossover mechanism to exchange genetic information between gametes. The crossover point on two parent chromosomes is chosen with assumed crossover probability. Apart from that random process genetic information can be modified through mutations. They also are random and occur with prescribed mutation probability.
Package for machine learning - OptFinderML.