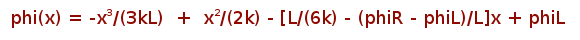1D Linear Differential Equations - Finite Element Method

1D - Boundary Value Problem

Boundary value problem to solve

differential equations, linear, lde, finite element method, fem, analytical solution, boundary value problem, Octave, Matlab, taketechease

where external force

for x in [0, L] and boundary conditions are: phi(0) = phiL, phi(L) = phiR.
The problem is trivial and can be easily solve analytically.

Analytical solution.

The solution reads:

Because of its simplicity the presented problem is a good example to test the numerical solution obtained with help of fem1D_lde.m program (written in Octave and Matlab code).

FEM solution.

FEM solution can be obtained from the Octave (MATLAB) program:

fem1D_lde.m consists of the function fem1D_lde(L, h1, NL, NI, NR, phiL, phiR, q, k, linear, varargin) where input arguments are:

L - domain length
h1 - length of edge compartments
NL - number of edge compartments at the left side
NI - number of internal compartments
NR - number of the edge compartments at the right side
phiL - left boundary value
phiR - right boundary value
q - force as anonymous function: @(x, L)(-2*x/L + 1)
k - coefficient
linear - can be set as 0 or 1; 0 means that QI vector is computed by integration whereas 1 means that it is obtained from linear approximation (see DEMO)
varargin - optional input arguments; the first from a set of variable input arguments is the analytical solution given as anonymous function: @(x, k, L, phiL, phiR) (-1/(3*L*k)*x.^3 + 1/(2*k)*x.^2 - (1/(6*k)*L - (phiR - phiL)/L)*x + phiL)

To test the finite element method try to consider the following situations:

NL = NR = 0, NI = 4;
How good is a numerical solution? How large is the element size h?
When is it useful to set NL and NR different from 0?
Is it a difference between QI vectors computed for different values of the parameter linear (0 or 1)?

Note! If do not feel quite familiar with the Octave (Matlab) language of programming and you do not want to go through them by your own you can always join the course: Introduction to Octave and Matlab. Let us see how easy and fast is programming using the Matrix Laboratory.